「また新しい公式が出てきた……」
「結局、この問題にはどれを使えば一番早いの?」
数学の宿題や模試の最中、そんな風にイライラしてペンが止まってしまったことはありませんか?
辺の長さ、角度、座標……。
問題によってバラバラに提示される条件を前に、「どの公式を召喚すべきか」迷っているうちに時間が過ぎていく。
その焦りが計算ミスを誘発し、結局最後まで解き終わらない。
そんな経験をしているあなたに、大切なことを伝えます。
三角形の面積は「暗記」で解くものではありません。
「条件分岐」で解くものです。
この記事では、元予備校講師の私が、どんな問題でも3秒で「最短ルート」の公式を特定できる逆引きフローチャートを伝授します。
もう、公式の多さに振り回されるのは今日で終わりにしましょう。
[著者情報]
数学戦略家・マサ先生
元大手予備校数学科主任。偏差値40台から東大・京大合格者を多数輩出してきた「効率化の鬼」。現在は数学学習コンサルタントとして、「計算量を最小限に抑える実戦的解法」を学生に伝えている。
教え子へのスタンス: 「努力が報われないのは君のせいではなく、武器の選び方を知らないだけだ」と寄り添い、実戦的な知恵を授ける。
なぜ「公式を覚えるほど」数学が解けなくなるのか?
「公式は全部覚えたはずなのに、テストになると手が動かない」。
これは、あなたが真面目に勉強しているからこそ陥る罠です。
教科書は、単元ごとに公式を教えます。
「三角比」の章ではsinを使う公式を、「平面図形」の章ではヘロンの公式を。
しかし、実際の試験では「どの単元の武器を使うか」は教えてくれません。
公式を「カタログ」としてバラバラに暗記していると、実戦でどの武器を手に取るべきか判断がつかなくなるのです。
私が受験生からよく受ける質問に、「全部の公式を完璧に覚えないとダメですか?」というものがあります。
私の答えはいつも同じです。
「重要な公式なんてない。その状況で『最も楽ができる公式』があるだけだ」と。
✍️ 専門家の経験からの一言アドバイス
【結論】: 公式を「覚える対象」から「条件で発動するプログラム」に書き換えてください。
なぜなら、この視点を持つだけで、問題文を読んだ瞬間に「あ、これはsinの出番だ」「これは座標の裏技だな」と自動的に解法が決まるようになるからです。迷いが消えれば、計算ミスは劇的に減ります。
【決定版】5秒で迷いが消える「面積公式・逆引きフローチャート」
では、具体的にどうやって公式を選べばいいのか。私が提唱する「最短ルート判定法」を公開します。
三角形の面積公式には、sin公式、ヘロンの公式、サラスの公式(たすき掛け)、ベクトルの面積公式など、多くの種類がありますが、これらはすべて「手元にあるヒント(条件)」によって使い分けが決まっています。
以下のフローチャートを頭に叩き込んでください。
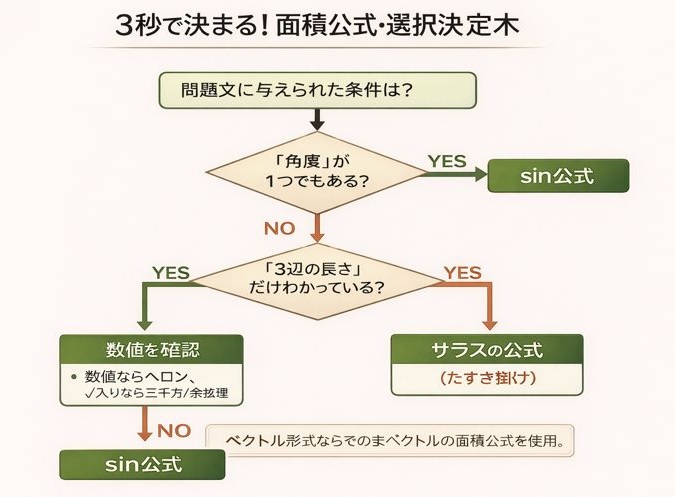
このフローチャートを使えば、sin公式とヘロンの公式は「角度の情報があるかないか」という排他的な関係にあることがわかります。
角度が1つでもあればsin公式、なければヘロンを検討する。
これだけで、迷いの半分は消えるはずです。
実戦攻略:その公式、本当に「最速」ですか?(地雷回避編)
公式を選んだ後にも、実は「地雷」が潜んでいます。
多くの受験生がハマる2つの罠を教えましょう。
1. ヘロンの公式の「√地雷」
「3辺がわかればヘロンの公式」と教わりますが、これには注意が必要です。
辺の長さに√(無理数)が含まれている場合、ヘロンの公式は計算地雷と化します。
二重根号の処理に追われ、10分以上浪費した挙げ句、計算ミスで終わるのがオチです。
詳しくはこちらで解説してます。
この場合は、あえて遠回りに見える「余弦定理でcosを出し、sinに変換する」ルートの方が、結果的に速くて正確です。
2. 座標問題の「サラス(たすき掛け)最強説」
座標平面上の三角形の面積を出すとき、学校では「2点を通る直線の方程式を出し、残りの点との距離(高さ)を求める」と教わります。
しかし、これはあまりに遅すぎます。
座標がわかっているなら「原点移動+たすき掛け(サラスの公式)」が圧倒的な上位互換です。
📊 比較表
【座標平面上の面積計算:標準解法 vs 最速解法】
| 比較項目 | 標準解法(点と直線の距離) | 最速解法(サラスの公式) |
|---|---|---|
| 計算ステップ数 | 約8〜10ステップ | 3ステップ |
| 所要時間(目安) | 3分〜5分 | 30秒 |
| ミスしやすさ | 高い(分数や2乗の計算多め) | 低い(単純な掛け算と引き算のみ) |
| 結論 | 検算用に使うべき | メイン武器として使うべき |
座標平面上の3点 (x_1, y_1), (x_2, y_2), (x_3, y_3) を頂点とする三角形の面積 S は、1点を原点に移動させた後の2点を (a, b), (c, d) とすると、 S = 1/2|ad – bc| で求められる。
出典: 高校数学の美しい物語 – 2024年参照
まとめ:武器を選べば、数学はもっと楽になる。
三角形の面積問題で大切なのは、公式をたくさん知っていることではなく、「今、どの武器を出すのが一番楽か」を判断する力です。
- 角度があればsin公式。
- 3辺が整数ならヘロン、√入りなら迂回。
- 座標なら迷わずサラス(たすき掛け)。
この判定基準さえ持っていれば、あなたはもう公式に振り回される側ではありません。問題をコントロールする側です。
さあ、今すぐ手元の問題集を開いて、このフローチャートを試してみてください。今まであんなに苦労していた計算が、驚くほどスルスルと解けるはずです。
[参考文献リスト]
- 三角形の面積を求める公式一覧 – 高校数学の美しい物語
- ヘロンの公式の使い方と計算ミスを防ぐコツ – 数スタ
- 座標平面上の三角形の面積 – 受験のミカタ
スポンサーリンク
