[著者情報]
滝沢 拓海 (Takumi Takizawa)
ゲーム理論アナリスト。元競技プログラマー。組合せ最適化と情報理論を専門とし、数多のパズルゲームをアルゴリズムで解明してきた。「運を嘆く前に論理を尽くせ」を信条に、エンジニア向けの戦略寄稿を行う。
友人との飲み会で興じた「ヒットアンドブロー」の対戦。
圧倒的なスピードで正解を射抜く友人を前に、「あいつは運が良かっただけだ」と自分を納得させてはいませんか?
もしあなたがそう感じているなら、エンジニアとして致命的な見落としをしています。
ヒットアンドブローは、数学的には平均5.21手で必ず終息する、極めて純粋な論理ゲームです。
友人が勝ったのは運ではなく、あなたの脳内にはない「フィルタリングのアルゴリズム」を回していたからに他なりません。
本記事では、情報理論に基づいた「期待値最大化戦略」を、我々エンジニアが実戦(脳内)で実行可能な5つの思考ステップへと変換して伝授します。
この記事を読み終える頃、あなたの「勘」は「確信」へとアップデートされ、次回の対戦では相手に「運の差」という言い訳すら許さない完勝を収めることになるでしょう。
なぜ「勘」では勝てないのか?ヒットアンドブローの正体は「情報フィルタリング」である
対戦中、あなたは無意識に「正解の数字を当てにいこう」としていませんか?実は、そのマインドセットこそが手数を増大させる最大の原因です。
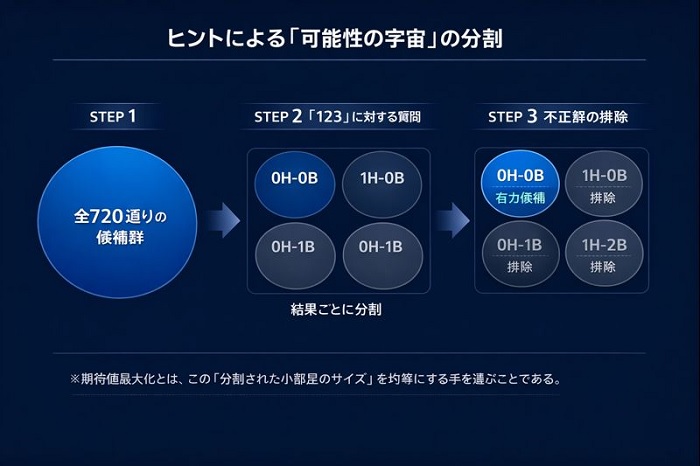
ヒットアンドブロー(3桁・重複なしルール)において、全パターンの宇宙は 10P3 = 720通り 存在します。
このゲームの本質は、正解を推測することではなく、「出されたヒント(H/B)を用いて、720通りの候補群をいかに効率よく切り刻み、死に体(矛盾する数字)を排除するか」という情報フィルタリングのプロセスにあります。
「1H-0B」という結果が返ってきたとき、それは単なるヒントではありません。
全候補のうち、その条件を満たさない数百通りの可能性が「一瞬で消滅した」ことを意味します。
勝負を分けるのは、このフィルタリングの精度です。
エンジニアがコードの計算量を削減するように、我々もまた、一手ごとに「残された候補数」を最小化する最適解を選択し続けなければなりません。
数学が導き出した最適解。平均5.21手で正解を射抜く「期待値最大化戦略」
最短手数で正解に辿り着くための鍵は、情報理論における「エントロピー(情報量)」の概念にあります。
情報量(エントロピー)を最大化する手を選ぶことは、フィルタリングの効率を極限まで高めることと同義です。
具体的には、次に提示する数字が「どのようなH/Bの結果を返してきたとしても、平均的に最も多くの候補を削れるか」を評価します。
これが「期待値最大化戦略」です。
数学者ドナルド・クヌースがマスターマインド(ヒットアンドブローの原型)に対して提唱したアルゴリズムを適用することで、平均手数は数学的限界である5.21手に収束します。
勘に頼るプレイヤーが8手、10手と彷徨う中で、論理を尽くす者は常に5手前後でゴールテープを切るのです。
実戦で使える「思考の5ステップ」。エンジニア流・脳内ソルバーの回し方
理論は理解できても、対戦中に複雑な期待値計算を脳内で行うのは不可能です。
そこで、我々人間が実戦で再現できる「思考のアルゴリズム」を5つのステップに構造化しました。
Step 1: 初期化 (Initialization)
初手は固定します。
数学的に最も効率が良いとされる「012」または「123」をデフォルトのクエリとして投げ、基準となる情報を取得してください。
Step 2: パースと仮説 (Parsing & Hypothesis)
返ってきたH/Bの結果から、特定の数字を「ヒット」だと仮定します。
例えば「1H-0B」なら、「1が位置も数字も合っている」という仮説を立てます。
Step 3: 矛盾のフィルタリング (Filtering)
立てた仮説に基づき、他の数字との整合性を検証します。
もし「1がヒット」とした場合に、前手までのヒントと矛盾が生じるなら、その仮説(=その数字の組み合わせ)は即座に破棄(フィルタリング)します。
Step 4: 期待値の選択 (Evaluation)
残った候補の中から、次の数字を選びます。
この際、「まだ使っていない数字」を1つ混ぜるのがコツです。
これにより、確定している数字の確認と、未知の数字の特定を同時に行い、情報量を稼ぐことができます。
Step 5: 収束 (Convergence)
候補が3〜5通りまで絞られたら、あとは全探索です。
論理的に矛盾しない数字を順に提示すれば、勝利は目前です。
【ヒント別・次の一手の定石(3桁重複なし・初手123の場合)】
| 返ってきたヒント | 状況の解釈 | 推奨される次の一手(戦略) |
|---|---|---|
| 0H-0B | 1, 2, 3は完全に除外 | 残りの「4567890」から3つ選ぶ。一気に候補が1/3以下に。 |
| 0H-1B | 1, 2, 3のうち1つが含まれるが位置が違う | 数字を1つずらし、新しい数字を2つ入れる(例:245)。 |
| 1H-0B | 1, 2, 3のうち1つが確定 | 1つを固定し、残り2つを入れ替える(例:145)。 |
| 0H-3B | 数字は全て正解、位置が全て不正解 | 3つの数字の順列(3! = 6通り)を入れ替えるだけで確定。 |
✍️ 専門家の経験からの一言アドバイス
【結論】: 「1H」が出た際、その1つを特定しようとして同じ数字を使い続ける「部分最適の罠」に注意してください。
なぜなら、この点は多くの人が見落としがちで、1つの数字を確定させるために1手使うよりも、他の可能性を同時に探る方が全体の期待値は高まるからです。私はかつて、特定の数字に固執するあまり、平均手数を2手も損していました。確定を急がず、常に「宇宙全体を削る」視点を持ってください。
【Q&A】初手は「012」が最強?重複ありの場合は?エンジニアが抱く疑問を解消
Q: 初手は「012」と「123」、どちらが数学的に優れていますか?
A: 3桁・重複なし・0使用可のルールであれば、数学的な期待値に有意な差はありません。重要なのは数字そのものではなく、その後のヒントに対して「どの数字が残っているか」を正確に管理するあなたのメモ能力です。
Q: 「重複あり」ルールの場合、戦略はどう変わりますか?
A: 候補数が 10^3 = 1000通り に増加し、フィルタリングの難易度が跳ね上がります。この場合、同じ数字を並べる(例:112)ことで、特定の数字が含まれる枚数を確定させるテクニックが有効になります。
Q: 4桁ルールで勝てません。
A: 4桁の場合、全候補は5040通りに膨れ上がります。脳内ソルバーだけでは限界があるため、マトリクス状のメモを使用し、各スロットごとの「可能性の有無」をビットフラグのように管理することをお勧めします。
まとめ:論理を尽くした者に、勝利は必然として訪れる
ヒットアンドブローは、決して運を競うゲームではありません。
出されたヒントという「入力」に対し、いかに効率的なフィルタリングという「処理」を行い、最短の手数という「出力」を得るか。
これは我々エンジニアが日常的に行っている最適化そのものです。
今回紹介した5つの思考ステップを意識するだけで、あなたの勝率は数学的限界まで高まります。
さあ、スマホを取り出して、あの友人に再戦を申し込みましょう。
論理の武器を手にしたあなたに、もはや「運」という言い訳は必要ありません。
[参考文献リスト]
- ヒットアンドブローの数学的考察 – Qualiteg
- Hit & Blow を解くアルゴリズム – Zenn, ponyo877 (2023)
- Mastermind Strategy – Wikipedia (Donald Knuth’s algorithm)
スポンサーリンク
