動画ばかり観てる暇人ブログ

ヘロンの公式はいつ使う？3辺から面積を「ミスゼロ・最短」で出す完全攻略ガイド

教養

[著者情報]
佐藤 先生
難関大受験数学専門・プロ家庭教師（指導歴15年）。偏差値40台から理系中堅〜難関大への逆転合格者を多数輩出。単なる公式の暗記ではなく、計算ミスを物理的に防ぐ「ノート術」と、試験時間を生み出す「解法選択の戦略」を教えるスペシャリスト。

「3辺の長さが 13, 14, 15……これ、余弦定理で解くの面倒だな」と、問題集を前に手が止まっていませんか？

教科書通りの「余弦定理でcosを出し、sinに変換して面積公式へ」という手順は、確かに王道です。

しかし、計算の手間が多い分、どこか一箇所で計算ミスをすればすべてが台無しになるリスクを孕んでいます。

結論から言うと、ヘロンの公式は「3辺が整数のとき」にだけ許された最強のショートカット武器です。

この記事では、15年の指導経験から導き出した「計算ミスを物理的に防ぐ書き方」と、数値を見た瞬間に解法を見抜く「0.5秒の判断基準」を伝授します。

この記事を読み終える頃には、ルートの中身がぐちゃぐちゃになってパニックになる自分を卒業し、試験中に「この数値ならヘロンで勝ちだ」と確信を持てるようになっているはずです。

目次

なぜ「ヘロンの公式」で差がつくのか？余弦定理ルートとの圧倒的な速度差

「公式を一つ増やすのは面倒だ」と思うかもしれません。

でも、想像してみてください。

試験の残り時間はあとわずか。

目の前には3辺が 13, 14, 15 の三角形。

ここで余弦定理ルートを選ぶと、まず15の2乗 = 13の2乗 + 14の2乗 ー 2・13 ・14cos Aという重い計算から始まり、cosを出し、さらにsin^2 A + cos^2 A = 1 でsinを求め……と、面積に辿り着くまでに少なくとも3〜4分はかかります。

その間に、隣のライバルはヘロンの公式を使い、わずか30秒で正解を書き込んで次の問題に進んでいるとしたらどうでしょうか？

ヘロンの公式と余弦定理は、どちらかが優れているのではなく、状況に応じて使い分ける「補完関係」にあります。

特に3辺が整数の場合、ヘロンの公式は圧倒的な時短を実現し、あなたの見直し時間を生み出してくれる「守護神」になるのです。

【0.5秒判断】ヘロンを「使うべき時」と「封印すべき時」の境界線

ヘロンの公式は強力ですが、万能ではありません。

無理に使うと逆に計算の地獄にハマります。

数値を見た瞬間に、以下のフローで解法を選別してください。

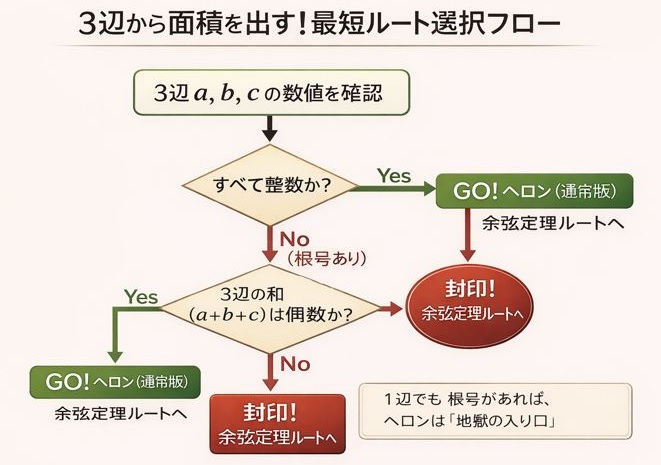
✍️ 専門家の経験からの一言アドバイス

【結論】: 3辺の中に一つでも√（根号）が含まれていたら、迷わずヘロンの公式を「封印」してください。

なぜなら、辺に根号がある状態でヘロンを使うと、ルートの中にルートが入る「二重根号」が発生し、高校数学の範囲では解けない、あるいは解くのに膨大な時間がかかる形になってしまうからです。この判断ミスが、試験中の爆死の最大の原因です。

 

プロが教える「ミスゼロ計算レイアウト」：$s$ の分数計算を消し去る魔法

ヘロンの公式で最もミスが起きやすいのは、実は公式そのものではなく、半周長 s = （a+b+c）/2が分数になったときの処理です。

多くの人が、分数のままルートの中に代入して通分でパニックになります。

これを物理的に防ぐのが、僕が推奨する「ミスゼロ・レイアウト」です。

📊 比較表
【計算ミスを防ぐ！ヘロンの公式・書き方の対比】

項目 多くの人がやる「ミスする書き方」 プロが教える「ミスゼロ・レイアウト」
sの扱い s = （13+14+15）/2 = 21 と、まず s を出す s を出さず、和の積として一気に書く
公式の形 S = √{s(s-a)(s-b)(s-c)} S = 1/4√{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}
メリット 教科書通りで覚えやすい 分数計算が一切消える。整数計算のみで完結。
リスク s が分数のとき、ルート内の通分でほぼ確実にミスる 公式が少し長く見えるが、計算自体は劇的に楽になる

特に3辺の和が奇数になり、s が「.5」になるようなケースでは、右側の「変形公式」が真価を発揮します。

計算用紙には、まず $a+b+c$ を書き、その横に「和から各辺を引いた値」を並べて書く。

このレイアウトを徹底するだけで、あなたの計算ミスは物理的にゼロに近づきます。

記述試験で使っても大丈夫？減点を防ぐための「書き方」と「証明」の要点

「ヘロンの公式を記述で使って減点されませんか？」という質問をよく受けますが、安心してください。

ヘロンの公式は、数学Iの検定教科書に発展的内容やコラムとして、あるいは例題として掲載されています。したがって、大学入試の記述試験において、証明なしでそのまま使用しても減点されることはありません。

出典: ヘロンの公式は記述で使える？ – 理系ラボ

ただし、上位校を目指すなら、一度は「余弦定理」からヘロンの公式を導き出すプロセスを自力でやっておくべきです。

なぜなら、入試では「公式そのもの」ではなく、「公式を導くプロセス（三角比の相互関係の利用）」を問う問題が出るからです。

「普段はヘロンで時短し、いざとなったら余弦定理で証明もできる」。

この二段構えの構えこそが、試験会場で揺るぎない自信を生みます。

まとめ：次の問題から「数値チェック」を始めよう

ヘロンの公式は、正しく使えばあなたの強力な味方になります。

  1. 3辺が整数なら「ヘロン」、根号があれば「余弦定理」。この0.5秒の判断を徹底すること。
  2. $s$ を分数にしない「変形公式」のレイアウトで、計算ミスを物理的に排除すること。
  3. 教科書掲載の公式として、自信を持って記述試験で使いこなすこと。

数学の成績を上げるコツは、難しい問題を解くことだけではありません。

こうした「確実に、素早く得点する戦略」を一つずつ積み上げることです。

今すぐ手元の問題集を開いて、3辺が整数の三角形を探してみてください。

そして、今日伝授した「プロの書き方」で、驚くほど簡単に面積が出る快感を体験してください！

[参考文献リスト]

スポンサーリンク