明日の数学の小テストに向けて、配布されたプリントを解いている健太さん。
公式を代入してみたものの、答えが合わずに「そもそもこれ、正弦定理で解くんだっけ?」とスマホを手に取ったのではないでしょうか。
余弦定理の公式は長くて複雑に見えますが、実は中学で習った「あの定理」の親戚にすぎません。
この記事では、プロ家庭教師として多くの学生を救ってきた私が、定理を3秒で選ぶ方法と、計算ミスを物理的にゼロにする手順を伝授します。
この記事を読み終える頃には、迷いなくペンが動くようになっているはずですよ。
[著者情報]
サトシ先生(プロ家庭教師)
「暗記ゼロの数学」を提唱する学習指導のスペシャリスト。偏差値30台の生徒を数多く名門大合格へ導く。自身も高校時代に数学で挫折した経験から、徹底的に「読者目線」に立った分かりやすい解説に定評がある。
読者へのスタンス: 「公式を忘れるのは君が悪いんじゃない、公式の『形』だけ覚えようとするからだ」と説き、健太さんの焦りに寄り添う。
なぜ余弦定理は「難しく」感じるのか?正体は三平方の定理の進化版
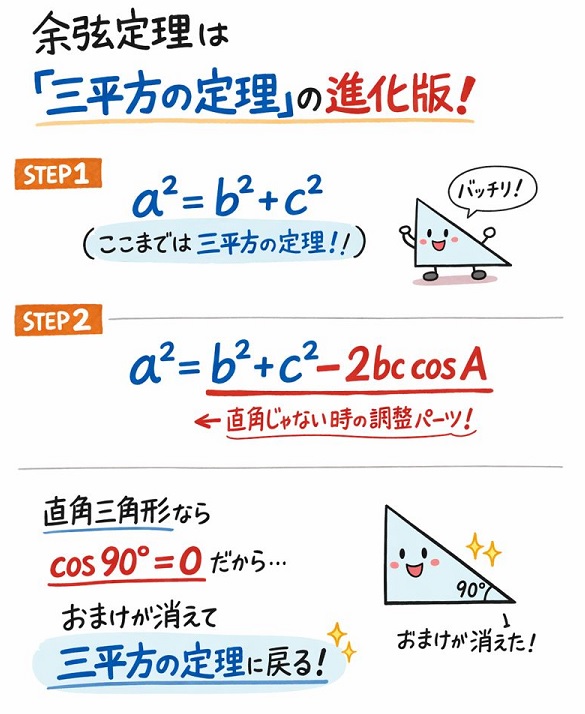
余弦定理の公式 a^2 = b^2 + c^2 – 2bc・cos A を見て、「うわっ、長い……」と拒絶反応を起こしていませんか?
実は、この公式の正体は非常にシンプルです。
公式の前半部分であるa^2 = b^2 + c^2 に注目してください。
これは中学で習った三平方の定理(ピタゴラスの定理)そのものです。
余弦定理とは、直角三角形でしか使えなかった三平方の定理を、「直角じゃない三角形でも使えるようにパワーアップさせた進化版」なのです。
後ろについている – 2bc・cos A は、直角からの「ズレ」を調整するための「おまけ」のようなもの。
そう考えると、少し気が楽になりませんか?
✍️ 専門家の経験からの一言アドバイス
【結論】: 公式を丸暗記しようとせず、「三平方の定理+調整パーツ」という構造で捉えてください。
なぜなら、この構造を理解していれば、万が一公式をど忘れしても「まずは二乗の和から始まるはずだ」と思い出すフックになるからです。私は高校時代、この構造に気づいてから公式が「ただの道具」に見えるようになりました。
【3秒判別】正弦定理とどっち使う?迷いを断つ「辺の数」チェック法
テスト中に最も多い悩みが、「正弦定理と余弦定理、どっちを使えばいいの?」というものです。
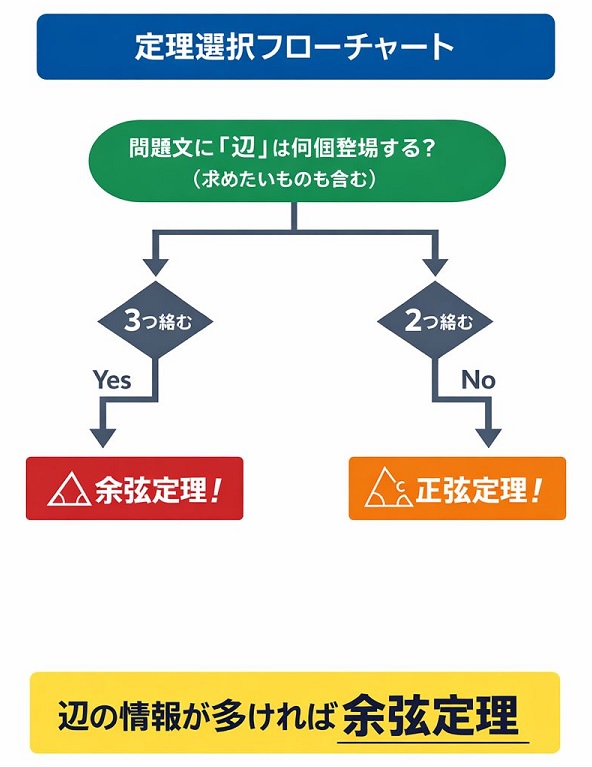
この二つの定理は、三角形の未知の要素を求めるためのライバル関係にありますが、実は「問題文に登場する辺の数」を見るだけで、3秒で決着がつきます。
結論から言いましょう。「辺の情報が多ければ余弦定理」です。
具体的には、以下のどちらかの条件に当てはまれば、迷わず余弦定理を雇用してください。
- 2辺とその間の角が分かっている(もう1つの辺を求めたい)
- 3辺がすべて分かっている(角の大きさを求めたい)
逆に、角の情報が多い(2角と1辺など)場合は正弦定理の出番です。
【ミス撲滅】もう間違えない!計算順序と「符号の壁」を突破する5ステップ
「式は立てられたのに、なぜか答えが合わない」という健太さん。
計算ミスの原因は、ほぼ間違いなく「計算の順番」か「$\cos$ の符号」のどちらかです。
特に多いのが、a^2 = 25 + 9 – 30 × 1/2 という式で、先に 25 + 9 – 30 を計算してしまうミスです。
掛け算(30 × 1/2)は引き算より先にしなければなりません。
この「魔の計算順序」を物理的に防ぐための、5ステップ・チェックリストを作成しました。
📊 比較表
表タイトル: 計算ミスの原因と対策
| ミスしやすいポイント | 正しい計算手順(5ステップ) |
|---|---|
| 1. 代入ミス | ① 公式に数値をそのまま代入する(暗算しない) |
| 2. 二乗の計算 | ② 各辺の二乗を先に計算する |
| 3. 順序の罠 | ③ 後ろの塊(2bc・cos A)を一つのパックとして計算する |
| 4. 符号の壁 | ④ cos が鈍角(マイナス)なら、符号を反転させる |
| 5. 最後の計算 | ⑤ 最後にすべてを足し引きする |
特にステップ④の「符号の壁」には注意が必要です。
cos 120度 のように角が 90度 を超える場合、値は必ずマイナスになります。
公式の「-2bc」のマイナスと、cos のマイナスがぶつかってプラスに変わる瞬間が、最大のミス発生ポイントです。
よくある疑問:cos 120度 がマイナスになるのが不安な君へ
「なぜ cos がマイナスになるの?」と混乱することもありますよね。
そんな時は、頭の中に「単位円(半径1の円)」を思い浮かべてください。
cos は、円の上の点の「横の位置(x座標)」を表しています。
- 90度 より小さい(鋭角)とき:点は右側にあるから、cos はプラス。
- 90度 より大きい(鈍角)とき:点は左側にあるから、cos はマイナス。
「左側だからマイナス!」と視覚的に覚えるだけで、符号のミスは劇的に減りますよ。
まとめ:明日のテストは「余弦定理」が得点源になる!
最後に、今日学んだ大切なポイントを復習しましょう。
- 余弦定理は「三平方の定理」の進化版。 構造で捉えれば怖くない。
- 「辺の情報が多い」なら余弦定理。 3秒で定理を選ぼう。
- 計算は「後ろの塊」を先に。 符号の変化には細心の注意を。
これで明日のテストの準備はバッチリです。
公式の長さに圧倒されず、まずは手元の問題集で「辺の数」を数えるところから始めてみてください。
一問解けるごとに、不安が自信に変わっていくはずです。
さあ、自信を持ってテストに臨んでください。
応援しています!
[参考文献リスト]
【関連記事】
スポンサーリンク
